Vectores en el espacio.
El término vector es empleado en ciencia y matemática para denotar una cantidad la cual tiene módulo (tamaño) y dirección. Algunas cantidades físicas como el desplazamiento, velocidades, fuerzas, entre otras son de naturaleza vectoriales (necesitan que se exprese su tamaño y dirección para quedar bien especificada). Si se pide que una persona realice una fuerza para mover un mueble ¿Hacia dónde debe la persona dirigir su esfuerzo físico? Piense en que se quería mover el mueble hacia la derecha y la persona dirigió su fuerza hacia la izquierda. ¿Se obtendrá el resultado esperado?
Un vector es un ente matemático que tiene módulo (magnitud) y dirección, descripto geométricamente con una semirecta o rayo (flecha de un solo sentido). El módulo representa “el cuánto” que tan grande o pequeño es el vector, la dirección es el menor ángulo medido al eje \(x\) positivo en sentido contrario a las agujas del reloj (si es en el plano), si es en el espacio a través de los ángulos que forma el vector con los vectores canónicos (se estudian más adelante).
Representación de vectores.
Es posible representar un vector de distintas formas las más comunes y de uso en ciencias físicas y matemáticas son:
Como un segmento de recta dirigido desde un punto \(P\) hasta un punto \(Q\). donde \(P\) es el punto inicial (cola) y \(Q\) es el punto final (punta). Así en la figura de la izquierda (arriba) el vector \(\vec{PQ}\neq\vec{QP}\) ya que tienen igual dirección (ángulo medido al eje \(x\) positivo), pero sentido opuesto. Por una letra en negrita o por una letra con una flecha en dirección izquierda a derecha sobre ella, por ejemplo, \(\mathbf{u}=\langle u_1,u_2,u_3⋯u_n\rangle\) en forma de una matriz renglón (o columna si se desea) donde las coordenadas \(u_1,u_2,u_3\cdots u_n\) son llamadas componentes del vector.
Componentes de un vector.
En cuanto a la representación gráfica un vector puede ser en elemento del plano o del espacio. En el caso de que el vector pertenezca al espacio de coordenadas por convención se utilizará el sistema de coordenadas espaciales dextrógiro (sistema derecho) como se muestra en la figura ###. Sea el punto \(P\left(p_1,p_2\right)\) y sea el punto \(Q\left(q_1,q_2\right)\) en el plano o \(P\left(p_1,p_2,p_3\right)\) y \(Q\left(q_1,q_2,q_3\right)\) si es en el espacio, las componentes del vector \(\mathbf{u}\) que va desde \(P\) hacia \(Q\) quedan determinadas como,
Un vector \(\mathbf{u}\) por componentes.
1. En el plano \(\mathbf{u}=\langle q_1-p_1,q_2-p_2\rangle =\langle u_1,u_2\rangle~~~~~~~~~~~~~~~~~~~~~~\)
2. En el espacio \(\mathbf{u}=\langle q_1-p_1,q_2-p_2,q_3-p_3\rangle=\langle u_1,u_2,u_3\rangle\)
Módulo o magnitud de un vector.
Sea \(\mathbf{u}\) un vector cualquiera entonces el módulo o longitud del vector también llamada magnitud o norma por algunos autores se define como la raíz cuadrada de la suma de los cuadrados de sus componentes, esto es,
Módulo de un vector
\(u=\sqrt{{u_1}^2+{u_2}^2}~~~~~~~~~~~~\)(en el plano)
\(u=\sqrt{ {u_1}^2 +{u_2}^2 +{u_3}^2 }~~~~~\) (en el espacio)
Ver Ej1 de los Ejercicios I
Vector nulo o cero.
Se denomina vector cero o vector nulo al vector en el cual todas las componentes son cero y por tal razón su módulo es cero. Si el módulo de un vector \(\|\mathbf{u}\|=0\) entonces obligatoriamente \( \mathbf{u}=\mathbf{0}.\)
Para más contenidos y luego clic en la pestaña del contenido deseado.
Vectores unitarios.
Se dice que un vector \(\mathbf{u}\) es un vector unitario si el módulo del vector \(\mathbf{u}\) es uno, y por lo general se denota como \(\hat{\mathbf{u}}\), esto es \(\|\hat{\mathbf{u}}\|=1.\) Un vector unitario \(\hat{\mathbf{u}}\) en la dirección de otro vector cualquiera \(\mathbf{v}\) queda determinado al dividir las componentes del vector \(\mathbf{v}\) entre su módulo.
Vector unitario \(\hat{\mathbf{u}}\) en dirección \(\mathbf{v}\)
$$\hat{\mathbf{u}}=\frac{\mathbf{v}}{||\mathbf{v}||}=\frac{\mathbf{1}}{||\mathbf{v}||}\mathbf{v} $$
Ver Ej2 de los Ejercicios I

Vectores canónicos unitarios.
En términos de las coordenadas espaciales \(x,\ y,\ z,\) se definen los llamados vectores unitarios canónicos, \(\mathbf{i}=\langle 1,0\rangle;~~~ \mathbf{j}=\langle 0,1\rangle\) para el plano, mientras que en el espacio se definen como
\( \mathbf{i}=\langle 1,0,0\rangle;~~~\mathbf{j}=\langle 0,1,0\rangle;~~~\mathbf{k}=\langle 0,0,1\rangle\)
cuya descripción geométrica se muestra en la figura.
En función de estos vectores un vector \(\mathbf{v}\) se escribe como, \(\mathbf{v}=v_1\mathbf{i}+v_2\mathbf{j}+v_3\mathbf{k}\)
donde \(v_1,\ v_2,\) y \(v_3\) son las componentes del vector.
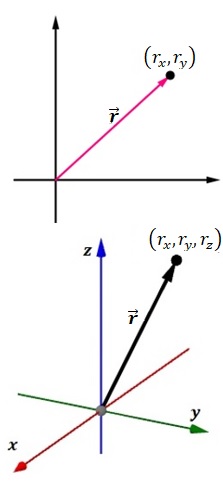
Vector de posición.
Se dice que un vector de posición es un vector dirigido desde el origen de coordenadas hasta un punto cualquiera (cola en el origen y afijo en un punto). Si un vector \(\mathbf{\vec{r}}\) está en el plano como se muestra en la figura de la izquierda sus componentes pueden ser escrita en función del ángulo \(\phi\) que forma con el eje de abscisa como, $$x=r\cos{\phi}; \ y=r\sin{\phi}$$ si el ángulo no está en posición normal, haciendo las proyecciones para completar el triángulo rectángulo y aplicando las definiciones de seno y coseno de un ángulo agudo se obtienen las componentes. Si se conoce la dirección \(\phi\) de un vector en el plano \(\mathbf{v},\) entonces un vector unitario en la dirección del vector \(\mathbf{v}\) es el vector $$\hat{\mathbf{u}}=\cos{\phi}\mathbf{i}+\sin{\phi}\mathbf{j}$$ Para el caso del espacio la descripción matemática es un poco más compleja, sin embargo, está pueda hacerse mediante el uso de los llamados ángulos directores del vector (ángulo entre cada uno de los ejes y el vector).
Sea \(\mathbf{\vec{r}}\) un vector de posición cualquiera en el espacio y sean \(\alpha\) (alfa), \(\beta\) (beta) y \(\gamma\) (gamma) los ángulos formados entre los vectores unitarios canónicos \(\mathbf{i},\ \mathbf{j}, \mathbf{k}\) y el vector \(\mathbf{\vec{r}},\) entonces las coordenadas del vector \(\mathbf{r}\) están dadas por, $$r_x=r\cos{\alpha};\ \ \ r_y=r\cos{\beta};\ \ \ \ r_z=r\cos{\gamma}$$ y el vector puede escribirse como $$\mathbf{\vec{r}}=r\cos{\alpha}\mathbf{i}+r\cos{\beta}\mathbf{j}+r\cos{\gamma}\mathbf{k}$$ los cosenos de los ángulos directores son llamados cosenos directores.
Ver Ej3 de los Ejericios I
Para más contenidos y luego clic en la pestaña del contenido deseado.
Operaciones con vectores.
Múltiplo escalar de un vector.
En el contexto de los vectores los números son llamados escalares, así cualquier cantidad \(c|c\in\mathbb{R}\) es un escalar, el producto de un escalar \(c\) por un vector \(\mathbf{\vec{u}}\) está dado por
$$c \mathbf{\vec{u}}=\langle cu_x,cu_y,cu_z\rangle$$
Si el módulo de un vector \(\mathbf{\vec{u}}\) se multiplica por un escalar \(c\) (distinto de cero por convención) el resultado es un nuevo vector cuyo modulo es \(c\) veces el módulo del vector \(\mathbf{\vec{u}}\), de esto se concluye que,
Módulo de un múltiplo escalar
$$||c\mathbf{u}||=c||\mathbf{u}||~~~~~~~~~ (1. 3)$$
La demostración a esto es bastante simple, \begin{align} &c\mathbf{u}=\langle cu_x,cu_y,cu_z\rangle\\ &\left|\left|c\mathbf{u}\right|\right|=\sqrt{\left(cu_x\right)^2+\left(cu_y\right)^2+\left(cu_z\right)^2}=\sqrt{c^2u_x^2+c^2u_y^2+c^2u_z^2}\\ &\left|\left|c\mathbf{u}\right|\right|=\sqrt{c^2\left(u_x^2+u_y^2+u_z^2\right)}\\ &\left|\left|c\mathbf{u}\right|\right|=c\sqrt{\left(u_x^2+u_y^2+u_z^2\right)}\\ &\left|\left|c\mathbf{u}\right|\right|=c\left|\left|\mathbf{u}\right|\right|\end{align} cómo se quería demostrar.
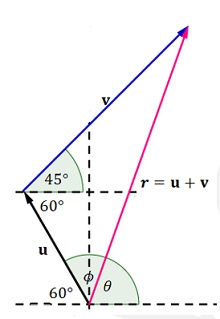
Adición de vectores. Método del triángulo.
Dados dos vectores en el plano \(\mathbf{\vec{u}}\) y \(\mathbf{\vec{v}}\) entonces su adición puede realizarse gráficamente al dibujar los vectores en el plano de modo que el punto inicial de \(\mathbf{\vec{v}}\) coincide con el punto final de \(\mathbf{\vec{u}}\), el vector \(\mathbf{\vec{r}}=\mathbf{\vec{u}}+\mathbf{\vec{v}}\) es el vector cuyo punto inicial coincide con el punto inicial de \(\mathbf{\vec{u}}\), y cuyo punto final coincide con el punto final de \(\mathbf{\vec{v}}\), la magnitud de \(\mathbf{\vec{r}}\) es la longitud de la línea trazada desde \( \mathbf{\vec{u}}\) hasta \(\mathbf{\vec{v}}\) la cual forma un triángulo con los vectores y por esta razón es que es llamado método del triángulo como se observa en la figura. Los valores analíticos se obtienen al aplicar la ley de los cosenos al vector suma.
Ver EJ4 Ejercicios I.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Dados los puntos \(P\left(2,\ 3,\ 5\right)\) y \(Q(8,6,10)\) determinar los vectores \(\mathbf{u}\) y \(\mathbf{v}\) que van desde \(P\) hacia \(Q\) y desde \(Q\) hacia \(P\) respectivamente al junto de sus módulos.
Determinar los vectores unitarios en la dirección $$ \mathbf{v_1}=\langle 3,5,7\rangle ~~~~~\mathbf{v_2}= \langle3,0,4\rangle ~~~~~~\mathbf{v_3}=\langle 3\sin{t},0,-3\cos{t}\rangle$$
Determinar los ángulos directores del vector \( \mathbf{r}=3\mathbf{i}+\mathbf{5j}+7\mathbf{k}\) y demostrar que \(\cos^2{\alpha}+\cos^2{\beta}+\cos^2{\gamma}=1.\)
Determinar la suma de los vectores \(\mathbf{u}=10.0m\) a \(120°\) con el este (referencia estándar) y \(\mathbf{v}=20.0m\) a \(45.0°\) con el Este, por el método del triángulo.
Determinar un vector de módulo tres en la dirección de \(\vec{\mathbf{v}}=\langle7,5,\sqrt{26}\rangle\)